import numpy as np
import tensorflow as tf
from tensorflow import keras
import matplotlib.pyplot as plt
import gym
env = gym.make("CartPole-v1")
class REINFORCE:
def __init__(self, env, path=None):
self.env=env #import env
self.state_shape=env.observation_space.shape # the state space
self.action_shape=env.action_space.n # the action space
self.gamma=0.99 # decay rate of past observations
self.alpha=1e-4 # learning rate in the policy gradient
self.learning_rate=0.01 # learning rate in deep learning
if not path:
self.model=self._create_model() #build model
else:
self.model=self.load_model(path) #import model
# record observations
self.states=[]
self.gradients=[]
self.rewards=[]
self.probs=[]
self.discounted_rewards=[]
self.total_rewards=[]
def hot_encode_action(self, action): '''encoding the actions into a binary list'''
action_encoded=np.zeros(self.action_shape, np.float32)
action_encoded[action]=1
return action_encoded
def remember(self, state, action, action_prob, reward): '''stores observations'''
encoded_action=self.hot_encode_action(action)
self.gradients.append(encoded_action-action_prob)
self.states.append(state)
self.rewards.append(reward)
self.probs.append(action_prob)
def _create_model(self): ''' builds the model using keras'''
model=keras.Sequential()
# input shape is of observations
model.add(keras.layers.Dense(24, input_shape=self.state_shape, activation="relu"))
# add a relu layer
model.add(keras.layers.Dense(12, activation="relu"))
# output shape is according to the number of action
# The softmax function outputs a probability distribution over the actions
model.add(keras.layers.Dense(self.action_shape, activation="softmax"))
model.compile(loss="categorical_crossentropy",
optimizer=keras.optimizers.Adam(lr=self.learning_rate))
return model
def get_action(self, state): '''samples the next action based on the policy probabilty distribution of the actions'''
# transform state
state=state.reshape([1, state.shape[0]])
# get action probably
action_probability_distribution=self.model.predict(state).flatten()
# norm action probability distribution
action_probability_distribution/=np.sum(action_probability_distribution)
# sample action
action=np.random.choice(self.action_shape,1,
p=action_probability_distribution)[0]
return action, action_probability_distribution
def get_discounted_rewards(self, rewards):
'''Use gamma to calculate the total reward discounting for rewards Following - \gamma ^ t * Gt'''
discounted_rewards=[]
cumulative_total_return=0
# iterate the rewards backwards and and calc the total return
for reward in rewards[::-1]:
cumulative_total_return=(cumulative_total_return*self.gamma)+reward
discounted_rewards.insert(0, cumulative_total_return)
# normalize discounted rewards
mean_rewards=np.mean(discounted_rewards)
std_rewards=np.std(discounted_rewards)
norm_discounted_rewards=(discounted_rewards-
mean_rewards)/(std_rewards+1e-7) # avoiding zero div
return norm_discounted_rewards
def update_policy(self): '''Updates the policy network using the NN model. This function is used after the MC sampling is done - following \delta \theta = \alpha * gradient + log pi'''
# get X
states=np.vstack(self.states)
# get Y
gradients=np.vstack(self.gradients)
rewards=np.vstack(self.rewards)
discounted_rewards=self.get_discounted_rewards(rewards)
gradients*=discounted_rewards
gradients=self.alpha*np.vstack([gradients])+self.probs
history=self.model.train_on_batch(states, gradients)
self.states, self.probs, self.gradients, self.rewards=[], [], [], []
return history
def train(self, episodes, rollout_n=1, render_n=50): '''train the model episodes - number of training iterations rollout_n- number of episodes between policy update render_n - number of episodes between env rendering '''
env=self.env
total_rewards=np.zeros(episodes)
for episode in range(episodes):
# each episode is a new game env
state=env.reset()
done=False
episode_reward=0 #record episode reward
while not done:
# play an action and record the game state & reward per episode
action, prob=self.get_action(state)
next_state, reward, done, _=env.step(action)
self.remember(state, action, prob, reward)
state=next_state
episode_reward+=reward
#if episode%render_n==0: ## render env to visualize.
#env.render()
if done:
# update policy
if episode%rollout_n==0:
history=self.update_policy()
total_rewards[episode]=episode_reward
if episode%10==0:
print(f"{episode} -> {episode_reward}")
self.total_rewards=total_rewards
r = REINFORCE(env)
r.train(200)
结果:
0 -> 39.0
10 -> 50.0
20 -> 18.0
30 -> 15.0
40 -> 16.0
50 -> 17.0
60 -> 20.0
70 -> 11.0
80 -> 20.0
90 -> 40.0
100 -> 36.0
110 -> 18.0
120 -> 79.0
130 -> 43.0
140 -> 41.0
150 -> 37.0
160 -> 95.0
170 -> 72.0
180 -> 138.0
190 -> 102.0
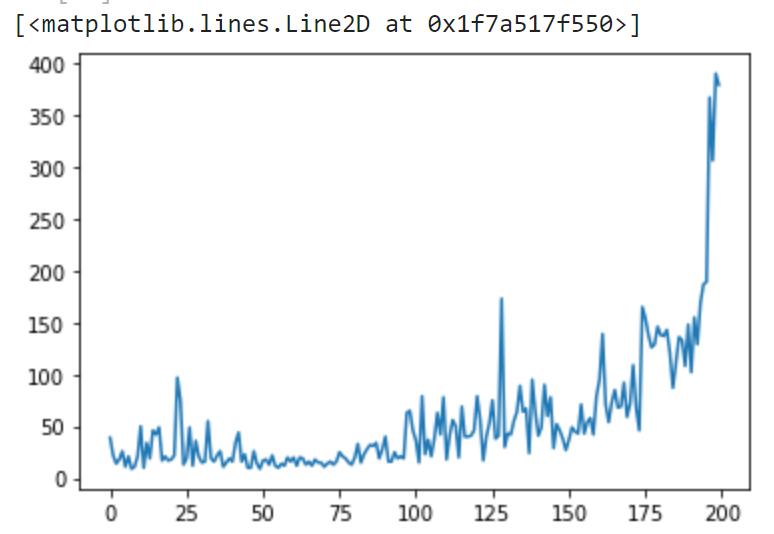
绘图:
plt.plot(r.total_rewards)
扩展学习:
-
训练山地车逃脱问题
-
TensorFlow训练RL实现CartPole平衡实验
-
CartPole滑冰问题
-
PyTorch训练RL实现CartPole平衡实验