import random
import matplotlib.pyplot as plt
import numpy as np
import math
import time
算法原理:
基因表示:解=基因形式编码(二进制,向量)
适应度函数:fit: Γ→R,越小越优
交叉:组合2父代解的基因生成子代解(单点交叉,多点交叉), Γ^2-> Γ
选择:勇士硬度函数筛选优质解(轮盘赌选择,锦标赛选择)
变异:随机扰动基因(翻转位,调整数值),避免陷入局部最优 ;Γ-> Γ
过程
1. 初始化种群:随机生成一组初始解(种群),G⊂Γ
2. 迭代进化:计算适应度(评估解),选择(保留高适应度个体),交叉变异(生成新一代种群),终止条件(最大迭代次或解收敛)
交叉操作细节:
随机选基因g1,g2,生成g=crossover(g1,g2);g适应度>g1和g2 -> 替代对应父代基因
变异操作细节:随机算g,换mutate(g)
GA可实现调度优化,最优装箱,最优切割,加速穷举搜索
公平分宝问题:钻石集合分成2子集,让子集总价值差最小
输入S -> S1,S,交集为空,最小化| ∑S1 - ∑S2 |
定义S:
N = 200
S = np.array([random.randint(1,10000) for _ in range(N)])
print(S)
结果:
[8344 2197 9335 3131 5863 9429 3818 9791 15 5455 1396 9538 4872 6549
8587 5986 6021 9764 8102 5083 5739 7684 8498 3007 6599 820 7490 2372
9370 5235 3525 3154 859 1906 8159 3950 2173 2988 2050 349 8713 2284
4177 6033 1651 9176 5049 8201 171 5081 1216 3756 4711 2757 7738 1272
5650 6584 5395 9004 7797 969 8104 1283 1392 4001 5768 445 274 256
8239 8015 4381 9021 1189 8879 1411 3539 6526 8011 136 7230 2332 451
5702 2989 4320 2446 9578 8486 4027 2410 9588 8981 2177 1493 3232 9151
4835 5594 6859 8394 369 3200 126 4259 2283 7755 2014 2458 8327 8082
7413 7622 1206 5533 8751 3495 5868 8472 6850 3958 3149 4672 4810 6274
4700 6134 4627 4616 6656 9949 884 2256 7419 1926 7973 5319 5967 9158
3823 7697 9466 5675 5412 9784 5426 8209 3421 1136 6047 4429 8001 4417
1381 722 7350 6018 6235 7860 5853 7660 5937 6242 1 9552 3971 8302
2633 9227 7283 154 8599 4269 9392 8539 1630 368 2409 9351 3838 9814
6186 5743 5083 1325 1610 779 3643 3262 5768 8725 961 4611 6310 4788
1648 5951 8118 7779]
这个后面再翻译:

代码:
def generate(S):
return np.array([random.randint(0,1) for _ in S])
b = generate(S)print(b)
结果:
[1 0 0 1 1 1 1 1 0 1 1 1 0 0 1 0 1 1 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1
0 1 1 1 0 1 0 0 1 0 0 1 1 0 1 0 1 1 0 0 1 0 0 0 1 1 0 1 1 0 0 0 0 1 0 1 0
1 0 0 0 0 0 1 1 0 1 0 0 1 0 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 1 1 0 0 0 0 1 1
1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 0 1 0 1 0 1 0 0 1 1 1 0 0 1 1
0 1 1 0 1 1 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 1 1 1 0 0 1 1 0 1 1 0 0 1 1 0
0 0 0 1 0 1 1 0 1 1 0 1 0 0 0]
定义fit函数,计算解的成本(S1总和和S2总和的差)
代码:
def fit(B,S=S):
c1 = (B*S).sum()
c2 = ((1-B)*S).sum()
return abs(c1-c2)
fit(b)
输出:
133784
变异:随机选一个bit取反
交叉:从两个父代染色体中随机算部分bit组合生成子代;生成随机掩码mask(决定子代bit来源)
变异率:控制变异发生概率
交叉率:决定会否交叉
代码:
def mutate(b):
x = b.copy()
i = random.randint(0,len(b)-1)
x[i] = 1-x[i]
return x
def xover(b1,b2):
x = generate(b1)
return b1*x+b2*(1-x)
创建初始解种群P,规模pop_size:
pop_size = 30
P = [generate(S) for _ in range(pop_size)]
n次迭代(进化),有30%变异,70%交叉
参数有三个:n_steps, mutation_rate, crossover_rate
函数返回最佳解=最佳基因,每次迭代种群最小适应度函数历史记录:
def evolve(P,S=S,n=2000):
res = []
for _ in range(n):
f = min([fit(b) for b in P])
res.append(f)
if f==0:
break
if random.randint(1,10)<3:
i = random.randint(0,len(P)-1)
b = mutate(P[i])
i = np.argmax([fit(z) for z in P])
P[i] = b
else:
i = random.randint(0,len(P)-1)
j = random.randint(0,len(P)-1)
b = xover(P[i],P[j])
if fit(b)<fit(P[i]):
P[i]=b
elif fit(b)<fit(P[j]):
P[j]=b
else:
pass
i = np.argmin([fit(b) for b in P])
return (P[i],res)
(s,hist) = evolve(P)print(s,fit(s))
输出:
[0 0 0 1 1 0 0 0 0 1 1 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 0 0 0 1 0 1 1 0
0 0 0 1 1 0 0 1 0 0 0 0 0 1 0 0 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 0 1 0 0 0
0 1 1 1 0 1 0 1 1 1 1 1 0 0 0 1 1 0 1 0 0 1 0 0 1 1 1 1 1 1 1 1 0 1 0 1 1
0 1 1 0 0 0 0 1 1 1 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 0 0 0 1 1 0 0 0 1 1 0 0
1 0 1 1 1 1 1 0 1 0 1 0 1 1 1 0 0 0 1 1 0 0 0 0 0 0 1 1 1 0 1 0 0 0 1 0 1
0 1 0 1 0 0 1 1 1 0 1 1 0 0 1] 4
总结:降低了适应度函数值
进化过程中种群适应度函数的变化趋势:
plt.plot(hist)
plt.show()
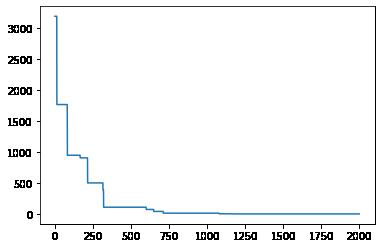
x = 迭代次=进化次,y = 适应度函数值
曲线 = 每代种群最小适应度值 = 反映优化
趋势:
初期快速下降 = 随机搜索快速找优解
中期波动 = 变异+交叉 -> 多样性(暂加适应度)
后期收敛 = 适应度稳定,接近最优解
N皇后问题:NxN棋盘放N和皇后,互不攻击(不在同一行/列/对角线)
全搜索解法:列表L(L[i]=第i行皇后的列位置),约束条件(每行1个皇后,互不攻击),找到第一个有效解就终止
步骤:生成排列(遍历所有列排列:每行1个列号) -> 验证对角线冲突(检查任意2皇后是否在同一对角线) -> 返回首个有效解(无冲突排列)
代码:
N = 8
def checkbeats(i_new,j_new,l):
for i,j in enumerate(l,start=1):
if j==j_new:
return False
else:
if abs(j-j_new) == i_new-i:
return False
return True
def nqueens(l,N=8,disp=True):
if len(l)==N:
if disp: print(l)
return True
else:
for j in range(1,N+1):
if checkbeats(len(l)+1,j,l):
l.append(j)
if nqueens(l,N,disp): return True
else: l.pop()
return False
nqueens([],8)
过程:[1, 5, 8, 6, 3, 7, 2, 4]
输出:True
解决N=20皇后问题要的时间:
%timeit nqueens([],20,False)
过程:10.6 s ± 2.17 s per loop (mean ± std. dev. of 7 runs, 1 loop each)
代码:
def fit(L):
x=0
for i1,j1 in enumerate(L,1):
for i2,j2 in enumerate(L,1):
if i2>i1:
if j2==j1 or (abs(j2-j1)==i2-i1): x+=1
return x
用GA结业N皇后:解=长度为N的L,适应度函数=互相攻击的N
def generate_one(N):
x = np.arange(1,N+1)
np.random.shuffle(x)
return (x,fit(x))
def generate(N,NP):
return [generate_one(N) for _ in range(NP)]
generate(8,5)
计算适应度函数耗时间,可以将种群的解和适应度值一起存
生成初始种群:
def generate_one(N):
x = np.arange(1,N+1)
np.random.shuffle(x)
return (x,fit(x))
def generate(N,NP):
return [generate_one(N) for _ in range(NP)]
generate(8,5)
输出:
[(array([2, 3, 8, 7, 5, 4, 1, 6]), 4),
(array([3, 4, 5, 1, 2, 8, 6, 7]), 8),
(array([1, 3, 7, 4, 5, 8, 6, 2]), 6),
(array([1, 5, 4, 6, 8, 3, 7, 2]), 4),
(array([3, 5, 7, 1, 8, 6, 4, 2]), 3)]
定义变异函数,交叉函数:
def mutate(G):
x=random.randint(0,len(G)-1)
G[x]=random.randint(1,len(G))
return G
def xover(G1,G2):
x=random.randint(0,len(G1))
return np.concatenate((G1[:x],G2[x:]))
xover([1,2,3,4],[5,6,7,8])
结果:
array([1, 2, 7, 8])
优先选择适应度更优基因增强基因选择过程:
基因被选中的概率取决于适应度
def choose_rand(P):
N=len(P[0][0])
mf = N*(N-1)//2 # max fitness fn
z = [mf-x[1] for x in P]
tf = sum(z) # total fitness
w = [x/tf for x in z]
p = np.random.choice(len(P),2,False,p=w)
return p[0],p[1]
def choose(P):
def ch(w):
p=[]
while p==[]:
r = random.random()
p = [i for i,x in enumerate(P) if x[1]>=r]
return random.choice(p)
N=len(P[0][0])
mf = N*(N-1)//2 # max fitness fn
z = [mf-x[1] for x in P]
tf = sum(z) # total fitness
w = [x/tf for x in z]
p1=p2=0
while p1==p2:
p1 = ch(w)
p2 = ch(w)
return p1,p2
GA进化循环:迭代至适应度函数=0找完美解,每轮生成新时代(跟当前的大小一样)
生成新时代:淘汰低适应度个体(_discard_unfit_function) -> 引入随机解(向世代添加随机生成的新解)-> 填充新时代
填充新时代细节:总大小_gen_size
按适应度比例随机选2个基因,适应度越高选中率越高;然后交叉,最后变异(_mutation_prob)
代码:
mutation_prob = 0.1
def discard_unfit(P):
P.sort(key=lambda x:x[1])
return P[:len(P)//3]
def nxgeneration(P):
gen_size=len(P)
P = discard_unfit(P)
P.extend(generate(len(P[0][0]),3))
new_gen = []
for _ in range(gen_size):
p1,p2 = choose_rand(P)
n = xover(P[p1][0],P[p2][0])
if random.random()<mutation_prob:
n=mutate(n)
nf = fit(n)
new_gen.append((n,nf)) ''' if (nf<=P[p1][1]) or (nf<=P[p2][1]): new_gen.append((n,nf)) elif (P[p1][1]<P[p2][1]): new_gen.append(P[p1]) else: new_gen.append(P[p2]) '''
return new_gen
def genetic(N,pop_size=100):
P = generate(N,pop_size)
mf = min([x[1] for x in P])
n=0
while mf>0:
#print("Generation {0}, fit={1}".format(n,mf))
n+=1
mf = min([x[1] for x in P])
P = nxgeneration(P)
mi = np.argmin([x[1] for x in P])
return P[mi]
genetic(8)
输出:
(array([4, 7, 5, 3, 1, 6, 8, 2]), 0)
GA优化N皇后问题时会快速收敛,局部最优陷阱;解决:限制迭代,动态调参,多线程或重启
快速收敛:快速找解(比全搜索好)
局部最优陷阱:偶发,算法长时间停滞
%timeit genetic(10)
结果:The slowest run took 18.71 times longer than the fastest. This could mean that an intermediate result is being cached.
26.4 s ± 28.7 s per loop (mean ± std. dev. of 7 runs, 1 loop each)
扩展学习:
-
丢番图实验